در مورد نسبت طلایی بیشتر بدانیم (1)

نسبت طلایی یا عدد فی ( Golden ratio) در ریاضیات و هنر هنگامی رخ می دهد که نسبت بخش بزرگتر به بخش کوچکتر، برابر با نسبت کل به بخش بزرگتر باشد.

تعریف دیگر آن از این قرار است که: عددی (ثابت) مثبت است که اگر به آن یک واحد اضافه کنیم، به مربع آن خواهیم رسید. همچنین تعریف هندسی آن چنین است: طول مستطیلی به مساحت واحد که عرض آن یک واحد کمتر از طولش باشد.

تعبیر هندسی عدد طلایی:

همان طور که اشاره شد برای محاسبه عدد طلایی باید نسبت بخش بزرگتر به بخش کوچکتر، برابر با نسبت کل به بخش بزرگتر باشد.

پیشینه

پیشینه توجه به عدد طلایی نه به زمان فیبوناچی بلکه به زمانهای بسیار دورتر می‌رسد. اقلیدس در جلد ششم از سیزده جلد کتاب مشهور خود که در آنها هندسه اقلیدسی را بنا نهاد، این نسبت را مطرح کرده‌است. لوکا پاچیولی در سال ۱۵۰۹ میلادی کتابی با عنوان نسبت الهی (The Divine Proportion) تألیف کرد. وی در آن نقاشی‌هایی از لئوناردو داوینچی آورده‌است که پنج جسم افلاطونی را نمایش می‌دهند و در آنها نیز به این نسبت اشاره شده‌است.

مصریان، سالها قبل از میلاد از این نسبت آگاه بوده‌اند و آن را در ساخت اهرام مصر رعایت کرده‌اند. بسیاری از الگوهای طبیعی در بدن انسان این نسبت را دارا هستند. نسبت طول ضلع پنج پر منتظم به طول ضلع پنج ضلعی منتظم برابر همین عدد است. روانشناسان هم بر این باورند زیباترین مستطیل به دید انسان، مستطیلی است که نسبت طول به عرض آن برابر عدد طلایی باشد. دلیل این امر آن است که این نسبت در شبکیه چشم انسان رعایت شده و هر مستطیلی که این نسبت را دارا باشد به چشم انسان زیبا می آید.

طبیعت

لئوناردو داوینچی اولین کسی بود که نسبت دقیق استخوان‌های انسان را اندازه‌گیری نمود و ثابت کرد که این تناسبات با ضریب عدد طلایی هستند.

کپلر (Johannes Kepler 1571-1630) منجم معروف نیز علاقه بسیاری به نسبت طلایی داشت بگونه‌ای که در یکی از کتابهای خود اینگونه نوشت: «هندسه دارای دو گنج بسیار با اهمیت می‌باشد که یکی از آنها قضیه فیثاغورث و دومی رابطه تقسیم یک پاره خط با نسبت طلایی می‌باشد. اولین گنج را می‌توان به طلا و دومی را به جواهر تشبیه کرد». تحقیقاتی که کپلر راجع به مثلثی که اضلاع آن به نسبت اضلاع مثلث مصری باشد به حدی بود که امروزه این مثلث به مثلث کپلر نیز معروف می‌باشد.

نسبت طلایی در ایران

برج و میدان آزادی:طول بنا ۶۳ و عرض ان ۴۲ است که ۱٫۵=۴۲: ۶۳ و به عدد طلایی نزدیک می‌باشد. سبک معماری آن نیزطاق بزرگی است که تلفیقی از سبک هخامنشی و ساسانی و اسلامی است که منحنی آن با الهام از طاق کسری معماری ایران باستان را تداعی می‌نماید.

قلعه دالاهو، کرمانشاه:خطی از استحکامات به طول دو و نیم کیلومتر و عرض چهار متر با قلوه و لاشه سنگ به همراه ملات دیوار گچ را می‌سازد. سرتاسر نمای خارجی این دیوار با مجموعه‌ای از برج‌های نیم دایره‌ای شکل تقویت شده است. می‌دانیم۱٫۶=۵/۲: ۴ که همان عدد طلایی است.

بیستون از دوره هخامنشی، کرمانشاه:به طول ۵ کیلومتر و عرض ۳ کیلومتراست. اعداد۵و۳هردوجزودنباله فیبوناتچی هستندو۱٫۶=۵:۳ و ابعاد برجسته کاری ۱۸ در ۱۰ پاست که قامت "داریوش"۵ پا و ۸ اینچ (۱۷۰ سانتیمتر) بلندی داردکه هر دو اعداد فیبوناتچی هستند.

یکی از هنرهای معماری در تخت جمشید این است که نسبت ارتفاع سر درها به عرض آنها و همین‌طور نسبت ارتفاع ستون‌ها به فاصلهٔ بین دو ستون نسبت طلایی است. نسبت طلایی نسبت مهمی در هندسه است که در طبیعت وجود دارد. این نشانگر هنر ابرانیان باستان در معماری است.

پل ورسک در مازندران: این پل بر روی رودخانه ورسک در مجاورت سواد کوه بنا شد. بلندی این پل ۱۱۰ متر است وطول قوس آن ۶۶ متر می‌باشد(۱٫۶ = ۶۶: ۱۱۰).

مقبره ابن سینا:آرامگاه دروسط تالاری مربع شکل قرارگرفته که پله مدور (مارپیچ فیبوناتچی) و پایه‌های دوازده‌گانه برج را احاطه کرده‌اند. سطح حیاط باسه پله سراسری به ایوان متصل است. ایوان با دری به ارتفاع ۲/۳ متر و عرض ۹/۱ متر به سرسرای آرامگاه متصل است (۱٫۶=۹/۱: ۲/۳)در دو طرف سرسرا دو تالار قرار دارد یکی در جنوب که تالار سخنرانی و اجتماعات است؛ و یکی در شمال که کتابخانه آرامگاه است. طول تالار کتابخانه ۴۵/۹ متر وعرض آن ۷۵/۵ متر است(۱٫۶=۷۵/۵: ۴۵/۹)

ارگ بم:این بنا ۳۰۰ متر طول و ۲۰۰ متر عرض داشته و از ۲ قسمت تشکیل شده است. این دژ ۵ شیوه ساختاری از خشت خام دارد. (۳ و ۲ و ۵ اعداددنباله فیبوناتچی هستند)

میدان نقش جهان و مسجد لطف‌الله:در کتب اخیر، نویسنده جیسون الیوت بر این باور است که نسبت طلایی توسط طراحان میدان نقش جهان و در مجاورت مسجد لطف‌الله مورد استفاده قرار گرفته است.^[۳]

خوشنویی میرعماد حسنی:با بررسی اکثریت قاطع حروف و کلمات میرعماد متوجه می‌شویم که این نسبت به عنوان یک الگو در تار و پود حروف و واژه‌ها وجود دارد و زاویه ۴۴۸/۶۳ درجه که مبنای ترسیم مستطیل طلایی است، در شروع قلم گذاری و ادامه رانش قلم، حضوری تعیین کننده دارد.^[۳]

عدد فی و معماری ایرانی

گفته می‌شود که: «اگر فاصله کعبه را در شهر مکه تا قطب شمال و جنوب اندازه گرفته و به هم تقسیم کنید عدد فی بدست خواهد آمد. برای اطمینان می‌توانید از نرم‌افزار Google Earth استفاده کنید و به این حقیقت دست یابید.» کعبه در لتیتودِ ۲۱٫۴۲۲۴۹۴۵ می‌باشد که به تناسبِ (۹۰–۲۱٫۴۲۲۴۹۴۵)/(۹۰+۲۱٫۴۲۲۴۹۴۵) برابر با ۱٫۶۲۴۷۶۷۳۹ می‌باشد که با عددِ فی تطابق دارد. از لحاظ کیلومتری مطابق با این صفحه از سایت مرکز مطالعات و پژوهشهای فلکی که به محاسبه قبله و مسافت شهرها از کعبه اختصاص دارد فاصله کعبه از قطب شمال 7626 و از قطب جنوب 12390 کیلومتر است که حاصل تقسیم این دو عدد برهم نیز ۱٫۶۲۴۷ خواهد شد. با فرض دقت اعداد ارائه شده در این سایت نقطه فی تنها در حدود 50 کیلومتر با کعبه فاصله دارد.

تاکنون نه تنها در کتاب رمز داوینچی بلکه پیام‌ها، اسرار مذهبی و کهن در دیوارهای زیارتگاه‌های اسلامی به صورت رمز قرار مشاهده شده است. بسیاری از کاشیکاری‌های بناهای اسلامی متعلق به ۵۰۰سال پیش توانسته‌اند الگوهای فراوان ریاضی پیدا کنند که تا دهه ۱۹۷۰ برای غربی‌ها ناشناخته بوده است. اساس یک طراحی هندسی برای نشان دادن یک نماد از علم «ماندالا» است که به عقیده بسیاری از ملت شرق به تعمق و اندیشه کمک می‌کند خلق بسیاری از نامحدودها با استفاده از مثلث و مستطیل طلایی از این گونه است

کیث کریچلو" keith Critchlowنویسنده کتاب "الگوهای ریاضی اسلامی" چنین ادعا می‌کند: ما دریافته‌ایم که اسلام در دوره قرون وسطی تا چه اندازه پیشرفته بوده است. نام این الگوهای ریاضی پیچیده در آن دوران "شیمی بیضی متقارن ممنوعه" می‌نامند. آنها از الگوی کاشی‌های هرمی برخوردارند و با چرخش یک سوم در آن قابل شناسایی هستند. همین قانون برای کاشی‌های مستطیلی نیز پیروی می‌کند که با چرخش یک چهارم قابل شناسایی هستند ما برای کاشی‌های شش گوش چرخش یک ششم لازم است. اما این شبکه‌ها بدون وجود پنج‌ضلعی‌ها کامل نمی‌شوند و بدون رعایت فاصله میان آنها در کنار هم جفت نمی‌شوند و نمی‌توان آنها را با با چرخش یک پنجم در کنار هم قرار داد. آقای لو توانست در دیوار یکی از زیارتگاه‌های ایران دو نوع از این کاشیکاری‌ها بزرگ را که با کاشی‌های هم‌شکل ساخته شده بود، کشف کند به گونه‌ای که ظاهراً از نسبت طلایی فیثاغورثی تبعیت می‌کردند. کریچلو در این‌باره می‌گوید: سازندگان بنا بطور حتم از این نسبت خبر داشتند.

در سال ۱۹۷۳سر «راجر پنروس» Roger Penroseریاضی‌دان برجسته غربی توانست با در نظر گرفتن این پنج‌ضلعی‌ها الگویی پنج تایی با شکلی بسازد که از آن به عنوان کیت و یا دارت نام برده می‌شود. او نخستین غربی بود که این حساب را کشف کرد و در آن زمان گمان می‌کرد نخستین کسی است به این موضوع پی برده‌است. خلاقیت وی به خلق خواص ریاضیاتی منجر شد هر دسته می‌تواند حاوی تعداد مشخصی‌از کیت‌ها و دارت‌هایی باشد که می‌توانند تا بی‌نهایت و بدون تکرارپذیری الگوهای کوچکتری از کیتها و دارت‌ها بسازند. هر چقدر تعداد این اشکال ریز افزایش پیدا کند آنگاه نسبت کیت‌ها به دارت‌ها به نسبتی موسوم به «نسبت طلایی» می‌رسد.

"گلرو نجیب اوغلو" Gulru Nacipogluیکی از اساتید دانشگاه هاروارد می‌گوید: خلقت انسان مشابه هم است و شکل مشخصی دارد که از عجایب خلقت خداوندی است این که این الگوها به کجا ختم می‌شوند و به صورت هوشمندانه‌ای در درها و پنجره‌ها به کار رفته‌اند مسئله‌ای است که نمی‌توان مشخص کرد. به گفته وی، با وجود این که الگوی پنروس به قرن ۱۴یا ۱۵بازمی‌گردد اما این اشکال کاشیکاری در دنیای اسلام از صدها سال قبل از آن به کار گرفته شده است. در منبتکاری‌های ایران در قرن پانزدهم و اوایل شانزدهم فهرستی از بسیاری از این طرح‌ها قرار دارند که ممکن است سرنخی برای شکوه ریاضیات اسلامی در مساجد ایران و ترکیه و مدارس بغداد و زیارتگاه‌های هند و افغانستان باشد. دانشمندان اکنون می‌دانند که مسلمانان در آن دوران می‌توانستند معادلات جبری به توان ۳و فراتر از آن را حل کنند معادلاتی که بسیار دشوارتر از معادله دو مجهولی است و اساس جبر به شمار می‌رود. مسلمانان همچنین دارای حسابگرهای مکانیکی بودند و در علم داروشناسی و ستاره‌شناسی پیشرفته‌تر از اروپایی‌ها بوده‌اند اما با این حال جای تاسف است که تعداد اندکی از این دانشمندان دربارهٔ یافته‌های خود کتاب و یا اثر به رشته تحریر درآورده‌اند".

ترسیم

برای رسم کردن مستطیل طلایی ابتدا مربع ABCD با استفاده از ضلع کوچک رسم می‌شود. سپس ضلع AB را نصف کرده، از وسط آن (نقطه G) باپرگار یک قوس به شعاع GC ترسیم کرده و ضلع بزرگ مستطیل (AE) را به دست می‌آورند. با توجه به شکل ترسیم شده، نصف طول این ضلع برابر نسبت طلایی است.

محاسبات:

برای محاسبه ی نسبت طلایی راه های متعددی وجود دارد که من به سه راه آن در اینجا اشاره می کنم:

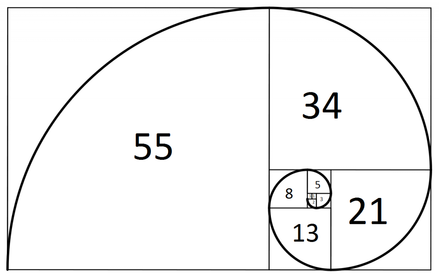
1.حد نسبت دنباله ی فیبوناچی:

دنباله ی فیبوناچی به شرح زیر است:

.....,1,1,2,3,5,8,13,21,34,55,89

در این دنباله هر جمله از جمع دو جمله قبلی به دست می آید اگر این دنباله را تا تعداد زیادی ادامه دهیم آن گاه حاصل تقسیم آخرین جمله ای که نوشته ایم بر جمله قبلی خود برابر نسبت طلایی خواهد شد.

2. با استفاده از نسبت هندسی و حل معادله درجه دو از روش دلتا:

3. با استفاده کسر مسلسل زیر:

انشاالله در پستی دیگر با عکس های متنوع در مورد این نسبت زیبا در خدمتتان خواهیم بود.